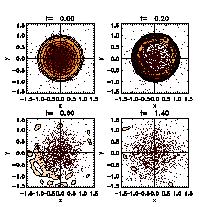Gas Expulsion from Star Forming Regions and the Formation of Globular Clusters

M. P. Geyer and A. Burkert

Abstract

Shortly after the formation of a Globular Clusters (GC) the remaining gas will be expelled by ionizing radiation, stellar winds or supernova explosions during a few dynamical timescales. As a result of this gas expulsion phase some or all stars in the cluster will get unbound. We have investigated the conditions necessary for obtaining bound stellar clusters.

In general, the fraction of finally bound stars is mainly determined by the timescale of the gas expulsion and the star formation efficency (SFE) 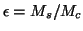$\epsilon = M_s/M_c$ $\epsilon = M_s/M_c$, where Ms and Mc are the mass of the stellar part and of the initial gas cloud prior to star formation, respectively.

Two sets of numerical N-body simulations are presented: As a first simplified approach we treat the residual gas as an external potential. The gas expulsion is approximated by reducing the gas mass to zero on a given timescale, which is treated as a free parameter. This process leads to an expansion and/or disruption of the system. Our results are consistent with similar simulations by Lada et al. (1984) and more recently by Goodwin (1997) and allow us to quantify the SFE necessary for forming bound GCs.

A new set of simulations has recently been started using smoothed particle hydrodynamics (SPH) to describe the residual gas more properly.

The Gas Expulsion Phase - Collisonless N-body Simulations

Our simulations start after the GC has been formed, but before the residual gas has been expelled. The stars of the GC are represented by collisonless, equal mass N-body particles following a King (1966) profile (Tab. 1). The effect of the ejection of the residual gas on the stellar system is treated as a time variable external potential, similar to the approach of Lada et al. (1984).

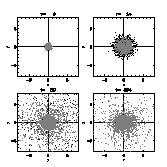
Figure 1
Small Animation
animation available: fast (92 kb) or slow (274 kb)
Figure 1: Typical evolution of the N-body part of a cluster (N3) with texp=2 and SFE $\epsilon =0.4$. Starting at t=20 the external potential is slowly reduced to zero within the gas expulsion time.

The cluster expands. A certain amount of stars gets unbound (dark dots) and starts leaving the system. The bound ones (light dots) relax after the gas has been completely removed, forming a broader configuration.

model c tc Rt N $\delta$
N1 0.67 0.28 1.26 1000 0.1
N2 1.05 0.17 1.33 1000 0.1
N3 0.67 0.28 1.26 4000 0.05
Table 1: Parameters of the initial configurations; c: concentration; tc: crossing time at half-mass radius; Rt: tidal radius; N: number of particles; $\delta$: smoothing length;

Figure 2: Time evolution of the Lagrangian radii containing 10% and 50% of the current bound mass of the system shown in Fig. 1. The constant mass radii before gas expulsion show that initially the system is in virial equilibrium. After the superimposed gas potential decreases (t>20), the mass radii increase rapidly and then relax (t>texp). The system achieves a more extended equilibrium state.
Figure 2

Radial Expansion of Globular Clusters

The radial expansion factor of the GC can be estimated as follows: In the adiabatic case (expulsion timescale is much longer than the crossing time) $R\, \cdot M$ is constant and therefore the ratio of final to initial radius is $R_f/R_i=1/\epsilon$. If the expulsion time is short compared to the crossing time, Hills (1980) obtained $R_f/R_i=\epsilon/(2\, \epsilon -1)$.

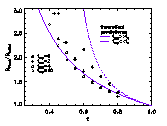
Figure 3: ratio of the final to the initial half-mass radii of the current bound particles of the simulations (model N3) for various expulsion timescales texp.
As expected, the simulations with slow gas expulsion fit well the solid curve, representing the adiabatic case. For high SFEs, the models with fast gas expulsion are in good agreement with the dashed curve, which holds when the expulsion time is less than the crossing time.
Figure 3

Stability of Globular Clusters after Gas Expulsion

After the gas expulsion the system of the remaining bodies relaxes again (see Fig. 2). The ratio of bound to unbound stars gives a threshold for the SFE $\epsilon$ necessary to form bound clusters.

Figure 4
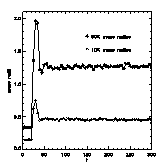
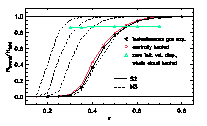
Figure 4:Ratio of the number of bound stars to the inital number of stars in the relaxed system after gas expulsion. Each symbol represents one run with given SFE and gas expulsion time.

The figure compares the initially more concentrated King model (N2) to the less concentrated one (N1). We find that the curves of model N2 are shifted to lower SFEs or higher ratios of bound stars, respectively. This is due to the lower half-mass crossing time of the more concentrated cluster N2 (Tab. 1). Thus, more concentrated clusters have a larger chance to survive. Large dots show results from Lada et al. (1984) obtained from simulations with 50 (!) stars.

In case of instantaneous gas expulsion the curves are centered around the theoretical limit $\epsilon=0.5$ for bound clusters in agreement with Hills (1980).
The number of finally bound stars increases with the gas expulsion time. In order for more than 50% of all the stars to remain bound the SFE must be equal to 45%, 30%, 25% and 20% for gas expulsion times texp =0, 2, 4 and 10, respectively.

Combined N-body and Hydrodynamical Simulations

We extended our simulations using smoothed particle hydrodynamics (SPH). Initially we adopted a pressure-confined, isothermal Bonnor-Ebert (BE) sphere (Ebert 1955; Bonnor 1956). To get a combined system of gas and stars, we added N-body particles with an equal density distribution, scaling the masses of the stars and the gas according to the SFE
$\epsilon$. We assigned the N-body particles a velocity dispersion according to the temperature of the gas. Isothermal spheres extend to infinity. In order to get a finite configuration, the gas density was set to zero at an arbitrary radius and an external pressure was applied.

Figure 5
Figure 5: Time evolution of model S2 (Tab. 2); SFE $\epsilon =0.4$, centrally heated; N-body particles projected onto the central x-y-plane of the cluster; light dots: bound particles; dark dots: unbound particles; contour lines indicate the gas density. In this scenario we heated up a small inner core, creating an outward propagating shock front disrupting the gas cloud.

model rh tc N T $\delta$
S1 0.7 0.8 2x4000 0.76 0.01
S2 0.7 0.8 2x11045 0.76 0.05
Table 2: Parameters of the initial configurations including gas dynamics; rh: half-mass radius; tc: crossing time; N: number of particles; T: gas temperature;
$\delta$: smoothing length;

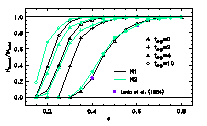
Figure 6: Ratio of the number of bound stars to the inital number of stars in the relaxed system after gas expulsion; dashed lines indicate the results from Fig. 4, model N3. The diamonds show the results for a cloud centrally heated by a factor of 200. The number of bound stars increased sligthly. However, the gas expulsion process is faster than the timescales adopted in the pure N-body simulations. The high SFEs needed to sustain a bound star cluster in this model can be avoided by forming stars with an initial zero velocity distribution, leading to a collaps of the GC and resulting in a nearly constant high ratio of bound stars (triangles).
Figure 6

Conclusions

N-body and combined N-body & SPH calculations to investigate the influence on the stellar part in star forming regions were presented. Gas expulsion will take place in general on a short timescale, of order the dynamical timescale. We confirmed that gas expulsion timescales which are several times longer than the crossing time of the GC can decrease the SFE needed to sustain bound clusters considerably.

However, our simulations including the proper dynamics of the residual gas show that in order to destroy the whole cloud the gas expulsion must take place on a shorter timescale, requiring a high SFE. Only few star forming regions show such high SFEs. To obtain bound clusters in low SFE regions may require compaction of cluster members with small initial velocity dispersion.

References

Bonnor, W. B. (1956). Boyle's Law and Gravitational Instability. MNRAS 116, 351-359

Ebert, R. (1955) . Z. Astrophys. 37, 217

Goodwin S. P. (1997). Residual Gas Expulsion from Young Globular Clusters. MNRAS 284, 785-802

Hills, J. G. (1980). The Effect of Mass Loss on the Dynamical Evolution of a Stellar System: Analytic Approximations. ApJ 225, 986-991

King, I. R. (1966). The Structure of Star Clusters III. Some Simple Dynamical Models. AJ 71, 64-75

Lada, C. J., M. Margulis & D. Dearborn (1984). The Formation and Early Dynamical Evolution of Bound Stellar Systems. ApJ 285, 141-152

Details
Kategorie: Kugelsternhaufen & Sternentstehung