Abstract

Using smoothed particle hydrodynamical simulations (SPH) we investigate the formation of stellar clusters in self-gravitating collapsing turbulent molecular clouds. We mimick star formation by creating N-body particles from gas particles in regions where the the gas density exceeds the Jeans criterion and where the gas flow is convergent.

Shortly after the formation of the first stars, the remaining gas will be expelled by energy feedback of the massive stars, like ionizing radiation, stellar winds or supernova explosions. As a result of this gas expulsion phase some or all stars in the cluster will get unbound. The fraction of finally bound stars is mainly determined by the efficiency of star formation and the timescale of the gas expulsion.

To follow the dynamical evolution of the young cluster during and after the gas expulsion, we simulate the energy feedback by heating up the gas particles surrounding the N-body particles at a constant rate. Star formation stops and the gas is expelled on a short timescale. We present two models with low and high heating rates. The conditions under which a massive globular cluster forms are investigated.

Setup, Star Formation & Feedback

We want to investigate the dynamics of a young star cluster during and shortly after its formation. To follow the formation process from scales as large as a molecular cloud down to the stars itself we need a recipe to mimick star formation. Different approaches concerning the inclusion of star formation in SPH simulations are discussed e.g. by Katz (1992), Bate (1995), Klessen (2000) and Nakasato et al. (2000).

Whenever the density of a gas particle exceeds the Jeans limit and the flow of the nearest neighbours is convergent, in our simulations a collisionless N-body particle is created with a mass according to a given intrinsic star formation efficiency. To avoid numerical problems, the intrinsic star formation efficiency is chosen in such a way that the mass of the new N-body particle is of order the gas particle mass. The mass of the gas particle and of its neighbours are reduced accordingly.

After a massive star has formed, it will feed back energy into the interstellar medium by ionizing radiation, stellar winds or supernova explosions. A survey of different methods implementing feedback in SPH is given by
Thacker & Couchman (2000). In our simulations each N-body particle contributes energy to its surrounding by increasing the thermal energy of the neighbouring gas particles at a constant rate.

Dynamical Evolution

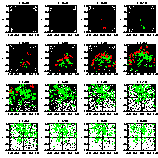
Time evolution projected onto the x-y-plane, high heating rate. Black dots represent gas particles, red dots are N--body particles created during the last timestep and green dots are N-body particles created in previous timesteps.

After the start of the simulation, the turbulence decays and the cloud starts collapsing. At t=0.6 the first stars form in high density regions. Their energy feedback expells the surrounding gas and causes star formation in the compressed medium in front of outwards propagating gas shells. N-body particles aligned on streaks appear if one gas particle forms several stars in short time intervals.

Star Formation Rate & Efficiency

Figure 2: Total number of N-body particles (upper curves at each case) and number of N-body particles with negative total energy (bound particles, lower curves). The simulation with high heating rate produces more stars than the simulation with low heating. However, most of the stars in the high heating rate case are formed in the cool compressed gas in front of the expanding gas shells due to the feedback of stars (see fig. 1). They gain high velocities and are not bound in the system of stars and gas. Thus the number of bound N-body particles in the high heating run declines faster with respect to the time than in the low heating case.

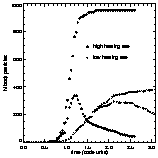
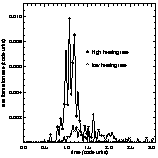
Figure 3: Star formation rate (mass of stars per time in code units). The simulation with high heating rate shows a strong peak due to the formation of stars in the outwards propagating gas shells.

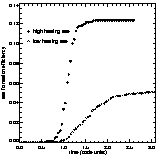
Figure 4: Ratio of the mass of the created stars to initial gas cloud mass (star formation efficiency). Our model shows only low star formation efficiencies, in accordance with observations. Thus, the star cluster that has formed is not likely to survive (Lada, Margulis & Dearborn, 1984; Geyer & Burkert, 2000)

Outlook

In future simulations we want to investigate the conditions necessary to obtain massive bound star clusters and compare the results to star forming regions and young globular clusters. High resolution runs are needed to examine the fragmentation and heating processes in detail.

References

Bate, M.R. (1995). The Role of Accretion in Binary Star Formation. PhD, Clare College, Cambridge

Geyer, M. P. & Burkert, A. (2000). The Effect of Gas Loss on the Formation of Bound Stellar Clusters. astro-ph/0007413, MNRAS, accepted

Katz, N. (1992). Dissipational Galaxy Formation. II. Effects of Star Formation. MNRAS 391, 502-517

Klessen, R.S. \& Burkert, A. (2000). The Formation of Stellar Clusters: I. Gaussian Cloud Conditions. ApJS 128, 287-319

Lada, C. J., M. Margulis & D. Dearborn (1984). The Formation and Early Dynamical Evolution of Bound Stellar Systems. ApJ 285, 141-152

Nakasato, N., Mori, M. & Nomto, K. (2000). Numerical Simulations of Globular Cluster Formation. ApJ 535, 776-787

Thacker, R.J. & Couchman, H.M.P. (2000). Implementing Feedback in Simulations of Galaxy Formation: A Survey of Methods. ApJ 545, 728-752